Петр Щедровицкий
Раздел 8. Машинизация мышления
Цифровая трансформация: как философские представления о «знаниях» помогают спрогнозировать ход новой промышленной революции?
Лекция 3. Проблема мышления: как создание
интеллектуальных машин может изменить мир
мыследеятельности
§ 60
После расщепления мыследеятельности на две названных составляющих появляется возможность повторить цикл мануфактуризации и машинизации – но уже по отношению к самой мыследеятельности управления машинами.
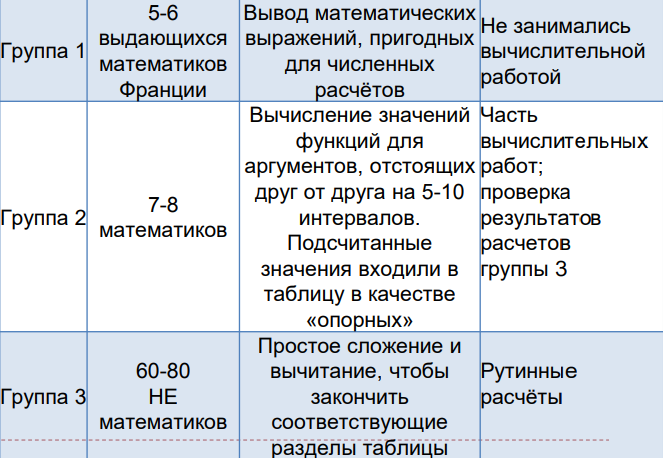
С 1792 года во Франции Гаспар де Прони экспериментирует с операционализацией и разделением труда в мыслительной деятельности для вычисления больших логарифмических и тригонометрических таблиц.
Существует исторический анекдот, согласно которому господин де Прони договорился с правительственными комитетами составить для сотенного деления круга логарифмические и тригонометрические таблицы, которые не только не оставляли желать лучшего в отношении точности, но и представляли собой самый большой и самый внушительный памятник вычислений, который когда-либо был выполнен или даже спроектирован.
Заказчики полагали, что для составления логарифмов чисел от 1 до 200 000 не хватит всей жизни «подрядчика», да и сам он уже пришёл в отчаяние от взятых на себя обязательств. Эти мысли крутились в его голове в тот момент, когда он, стоя перед книжным магазином, увидел прекрасное английское издание Смита, выполненное в Лондоне в 1776 году: он открыл книгу наугад и наткнулся на первую главу, в которой говорится о разделении труда и в качестве примера приводится изготовление булавок.
Едва он прочел первые страницы, как по какому-то вдохновению он изобрел способ изготовления своих логарифмов как булавок. Он уехал на несколько дней в деревню и вернулся в Париж с производственным планом. Он объединил две мастерские, которые отдельно произвели те же расчеты и использовали взаимную проверку.
Работы по расчету таблиц, считавшиеся невыполнимыми, завершаются менее чем через 10 лет, в 1801 году.
§ 61
Спустя 18 лет, в 1819 году, Чарльз Бэббидж посещает Францию и узнает об этом проекте по созданию таблиц логарифмов и тригонометрических функций.
30. Babbage Ch. «On the Economy of Machinery and Manufactures», 1832.
Опыт Прони вдохновляет Бэббиджа и он начинает двигаться в двух разных направлениях: с одной стороны, он мануфактуризирует деятельность по созданию таблиц, а с другой — ищет пути машинизации этой деятельности.
Позже Бэббидж в работе «On the Economy of Machinery and Manufactures» 1832 года напишет: «Мы уже упоминали то, что, может быть, покажется некоторым из наших читателей парадоксальным, что разделение труда может быть применено с одинаковым успехом к умственным, как и к механическим операциям, и что оно обеспечивает в обоих случаях одинаковую экономию времени»30.
30. Babbage Ch. «On the Economy of Machinery and Manufactures», 1832.
«Краткий отчет о его практическом применении в самой обширной серии вычислений, когда-либо проводившихся, будет служить интересной иллюстрацией этого факта, и в то же время даст возможность показать, что меры, которые должны регулировать внутреннюю экономику мануфактуры, основаны на принципах более глубоких, чем можно было бы предположить, и могут быть с пользой использованы для подготовки пути к некоторым из самых возвышенных исследований человеческого разума»31.
31. Там же
Вернувшись в Англию, Бэббидж вместе с Гершелем основал проект по созданию таблиц для вновь созданного астрономического сообщества.
При этом самые низкоуровневые вычисления основывались на оценке многочленов (скажем, разложением в ряд) с использованием разностного метода.
Бэббидж полагал, что может быть создано специальное устройство — разностная машина — которая сможет вычислять любой многочлен до определенной степени посредством специального метода и которая затем будет автоматически выдавать результат, сводя человеческий фактор, тем самым, к нулю.
Он принимает решение создать «разностную машину», которая могла бы реализовать расчеты, в том числе необходимые для создания логарифмических и тригонометрических таблиц.
В 1832 году, описывая основания своего решения, он напишет:
«Поскольку возможность выполнения арифметических вычислений с помощью машин может показаться читателям, не являющимся математиками, слишком большим постулатом и поскольку это связано с предметом разделения труда, я попытаюсь здесь в нескольких строках дать некоторое представление о том, как это можно сделать, и, таким образом, снять небольшую часть завесы, скрывающей эту кажущуюся тайну.
То, что почти все таблицы чисел, подчиняющиеся какому бы то ни было закону, каким бы сложным он ни был, могут быть образованы в большей или меньшей степени исключительно за счет правильного расположения последовательных сложений и вычитаний чисел, соответствующих каждой таблице, является общим принципом, который может демонстрироваться только тем, кто хорошо знаком с математикой; но ум даже читателя, который лишь немного знаком с этой наукой, легко поймет, что это не невозможно, обратившись к следующему примеру»32. Далее Бэббидж приводит пример расчета таблицы квадратных чисел.
32. Там же
В 1827-м таблица логарифмов, составленная вручную, наконец была закончена, после чего переиздавалась в неизменном виде в течение приблизительно ста лет.
§ 62
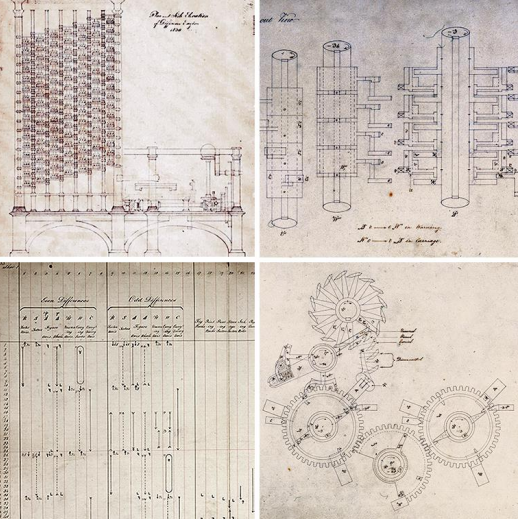
В 1822 году (то есть ровно 200 лет назад) Бэббидж демонстрирует прототип разностной машины, способной помимо 4-х арифметических операций осуществлять операции с кодами «команд».
Как и станком Жаккарда, операциями этой машины управлял не человек, а особый «управляющий элемент», который предварительно было необходимо «запрограммировать».
Машина «программировалась» с помощью «…позиционирования металлических штырей в цилиндре с отверстиями, который назывался контрольный цилиндр».
Для построения на следующем шаге аналитической машины Бэббидж нанял лучших инженеров своего времени. Но по каким-то причинам, несмотря на десять лет работы и множество высокоточных станков и инструментов, машина так и не была построена.
В отличие от разностной машины, «аналитическая машина» представляет из себя «компьютер общего назначения», то есть, прототип ЭВМ, но на другой материальной и элементной базе.
Устройство аналитической машины включало в себя 1) устройство управления последовательностью операций, помещением переменных на «склад» и извлечениям их из «склада», считывающее последовательность операций с перфокарт; 2) сам «склад» для хранения значений переменных, с которыми производятся операции, и результатов операций (память); 3) «мельницу» — аналог современного процессора, производящую операции над переменными и хранение в регистрах их значений, с которыми в данный момент осуществляются операции; 4) устройство печати и 5) устройство ввода результатов на перфокарты.
Программирование машины должно было осуществляться с помощью трёх перфокарт. Уже летом 1843 года Ада Лавлейс написала для неё «программу» в том более узком смысле, о котором мы говорили в самом начале.
Она рассуждает о циклах, циклах циклов (вложенных циклах), использовании циклов для уменьшения числа карт. Ее понятие «цикла» почти дословно совпадёт с приводящимся в современных учебниках программирования. В материалах Бэббиджа и Лавлейс намечены такие понятия, как подпрограмма и библиотека программ, модификация программ и индексный регистр.
Надо сказать, что по мере роста интереса к Бэббиджу в ХХ веке росло и любопытство касательно того, будет ли работать разностная машина, если её построить по чертежам Бэббиджа.
Подобный «эксперимент» был начат в 80-е годы ХХ века и в 1991-м, после титанических усилий, была построена законченная версия аналитической машины (а принтер добавили в 2000-м) лишь с одним исправлением в чертежах. Удивительно, но машина работала. Строительство обошлось примерно во столько же (с поправкой на инфляцию), сколько Бэббидж просил от британского правительства еще в 1823 году33.
33. Wolfram S. «Untangling the Tale of Ada Lovelace».
§ 63
Надо отметить, что уже 1826 году Бэббидж также строит язык описания операций механических машин, в том числе функционирования программируемой машины, который он называет «механическая нотация». Он описывает ее в статье «Методы обозначений машинных операций посредством знаков»34.
34. Babbage Ch. «On a Method of Expressing by Signs the Action of Machinery», 1826.
Для этого, по мнению Бэббиджа, надо выделить основные элементы машины, обозначить связи между ними, схематизировать процесс изменения состояний элементов во времени (часть изменяется непрерывно, а часть – дискретно), приписать определенным состояниям элементов машины статус «сигналов» и задать связь этих «сигналов» со знаками (в данном конкретном случае – математическими), а также обозначить операции с элементами, через которые на машину передаётся управляющее воздействие.
Результаты этой работы были описаны в статье «Методы обозначений машинных операций посредством знаков» на примере программирования работы гидравлического устройства.
§ 64
Как Вы поняли, мануфактуризация и машинизация определённых режимов мыслительной деятельности стали возможны благодаря использованию оперативных языков математики.
Можно сказать, что на уровне простых операций эти алгоритмы оказались в каком-то смысле значительно проще, чем алгоритмы вещественных преобразований. Список элементарных операций был ограничен небольшим числом базисных операций со знаками, на которые раскладывалась любая сложная операция.
После смерти Бэббиджа в 1871 году идея создания машины для вычислений на долгие 60 лет снимается с повестки дня промышленного развития. Идея «универсальных вычислений» вновь появляется только в работе Алана Тьюринга, посвященной математической логике, в 1936 году35.
35. Turing A. «On Computable Numbers, with an Application to the Entscheidungsproblem», 1936.
§ 65
Я бы выделил несколько основных причин, приведших к образованию такой вынужденной паузы:
Во-первых, только Вторая промышленная революция привела к созданию материальной и технической базы нового поколения умных машин — электронных ламп и полупроводников.
Во-вторых, задачи управления машинами потребовали разработки новых дополнительных средств и, прежде всего, новых знаковых систем и правил оперирования с ними;
Во-третьих, возникла необходимость более детальной прорисовки рабочей онтологии – представлений об интеллектуальных процессах, уже – процессах мышления, мыслительной деятельности и управления;
В-четвёртых, во второй половине XVIII века на смену более механистической объемлющей картине мира, которая была характерна для многих создателей новых наук в более ранний период, пришло более сложное «органическое» или «органистическое» мировоззрение.
Про совершенствование материальной и технической базы я специально не буду сейчас ничего говорить.
Напомню лишь, что первая физическая вычислительная машина (компьютер) включала в себя 18 000 ламп, а Тьюринг, по слухам, проводил отладку своих машин не выключая тока, чтобы не терять чувства реальности.
§ 66
В той мере, в какой для человека все вещи, с которыми он имеет дело, в большей или меньшей степени имеют семиотическую форму существования, второй круг задач был связан с разработкой специальных искусственных языков и правил манипулирования с ними.
Основное требование к этим знаковым системам состоит в том, чтобы знаки, с материалом которых будет иметь дело мыслительное манипулирование, могли включаться в системы простых преобразований. Другим словами, речь идёт о разработке оперативных языков, и, как следствие – операционализации и формализации мышления.
Как известно, уже в конце 40-х годов XIX века Джордж Буль закладывает основы для новой дисциплины — математической логики.
Развитие этих языков идёт достаточно медленно. Саймон говорит в своей Тьюринговской лекции 1975 года: «Наше современное понимание символьных систем прошло… несколько последовательных этапов. Формальная логика приучила нас к символам, рассматриваемым синтаксически, как сырой материал для мышления, а также к идее манипулирования ими (символами), согласно тщательно определёнными формальным процессам.
Машина Тьюринга сделала синтаксическую обработку символов по-настоящему механической и подтвердила потенциальную универсальность строго определённых символьных систем. Понятие хранимой программы для компьютера подтвердило интерпретируемость символов, уже неявно присутствующую в идее машины Тьюринга.
Обработка списков выдвинула на передний план денотационные возможности символов и определило обработку символов такими способами, которые допускали независимость от фиксированной структуры физического устройства (физической машины). К 1956 году все эти концепции уже были уже доступны, как и оборудование для их реализации. Могло начаться изучение интеллектуальности символьных систем — предмет науки об искусственном интеллекте»36.
36. Лекции лауреатов премии Тьюринга за первые двадцать лет: 1966-1985. Издательство «Мир».
Я понимаю, что для большинства из Вас эти рассуждения звучат как «китайские иероглифы». Поэтому позволю себе переформулировать их в языке СМД-подхода.
Создание искусственных (формальных) логических и логико-математических языков во второй половине XIX — начале ХХ века создавало надежду для представителей научного и инженерного сообщества, что управляемые машины нового типа могут программироваться на основе математических моделей, а сами управляющие действия могут быть описаны и с=программированы как преобразования параметров этих моделей.
Первоначально даже казалось, что эти алгоритмы преобразований окажутся значительно проще, чем алгоритмы вещественных преобразований материала деятельности. Ведь в данном случае материал не «сопротивляется», и с ним можно осуществлять практически любые преобразования.
Список простых преобразований в этом случаем может быть ограничен небольшим числом базисных операций со знаками, а любая «сложная» операция может быть составлена из простых.
Переход от простых символов к анализу «процессов» или «оперативных объектов» устанавливалось за счёт операций кодирования.
На уровне мета-представлений с 20-х годов стало использоваться понятия «меры информации» и «информации». В понятии «меры информации» (в отличие от понятия «знания») была заложена возможность абстрагироваться от содержания знаковых выражений: все, что могло сделать техническое устройство, должно было быть проинтерпретировано как превращение сигнала и выделение формальных различий между массивами данных, значимых с точки зрения принятия решений человеком или человеко-машинной системой.
Другими словами, эти сигналы приобретают характер «информации» в отличие от «шума» в той мере, в какой задействуются в процессах принятия решений человеком, и теряют его вне этих отношений. Представление машины в виде «информационной системы» позволило в дальнейшем ввести в рассмотрение инженерные модели, описывающие функции «данных», с одной стороны, «знаний», с другой стороны, как видов средств.
Технически задача сводилась к тому, чтобы построить механизмы, реализующие элементарные преобразования знаков, и организовать эти механизмы в системы, реализующие алгоритмы.
§ 67
В начале ХХ века из всей постепенно трансформируется трактовка интеллектуальных процессов и, в частности, «мышления» и «мыслительной деятельности».
Как я уже сказал выше, под мыслительной деятельностью в узком смысле слова стало пониматься прежде всего манипулирование и оперирование со знаками.
С этой точки зрения вопрос «может ли машина мыслить?» приобрёл своего рода перевёрнутый характер.
Именно вычислительная «машина» стала моделью, объективирующий ту небольшую часть интеллектуальных процессов, которую информатика и компьютерные науки стали называть «мышлением» в узком смысле этого термина — то есть мыслительной деятельностью со знаками.
Если на первом шаге исследователи ещё пытались описать реальную сложность интеллектуальных процессов, которые осуществлял человек, и «выделять» из них процессы мыслительной деятельности, то на более поздних этапах то, что мог делать компьютер или, шире, то, чему его можно было научить при определённых условиях, и было объявлено «мышлением».
На повестку дня встал вопрос о том, а мыслит ли в этом смысле (может ли мыслить) человек?
В конце 50-х-начале 60-х годов Марвин Минский сформулировал пять основных задач, которые, с его точки зрения, может решать машинный «интеллект»: это поиск, распознаванием образов, самообучение, планирование и индукция (индуктивный вывод)37.
37. Minsky M. «Steps toward artificial intelligence. Proceedings of the IRE», 49(1), 8-30, 1961.
§ 68
Во второй половине ХХ века обострился интерес к анализу двух подходов к описанию Мира и двух типов явлений и процессов — «механических» и «органических».
Если воспользоваться уже введённым нами выше понятием «управления», то можно сказать, что для работы «механизма» и «машины» управляющая программа осуществляемого ею процесса задается извне.
Напротив, «организм» или «органическая» система несёт на себе и постоянно корректирует управляющую программу своего поведения и действий.
Исходные версии новоевропейской науки и инженерии создавались под влиянием механических метафор: согласно этому подходу, «природа» по своему устройству может быть уподоблена «часам» и, будучи создана самым искусным часовщиком (Богом), может быть подвергнута ремонту и усовершенствованию человеком.
Однако, уже в работах Спинозы можно найти скептические замечания по этому поводу, а у Лейбница можно найти утверждения, что органические системы (организмы), в отличие от механических, характеризуются процессами самоорганизации и самоуправления.
Гёте развивает органическую картину мира, утверждая, что любой живой организм воспроизводит себя как представитель определённого рода (дерево как представитель рода деревьев), производит себя как индивидуума, а различные «части» (функциональные органы) этого организма устанавливают отношения друг с другом, производя «целое» так и таким образом, что сохранение одной части является условием сохранения других.
В основу новой картины мира, которая и сегодня продолжает складываться буквально на наших глазах, были положены представления об органических процессах, модели «эволюции» и «развития», интерес к потокам, вихрям, течениям и водоворотам (любопытны в этом плене исследования Леонардо да Винчи), понятия «случайности» и «самоорганизации».
Последняя стала трактоваться как реальность возможного, более широкая, нежели актуализированная действительность явлений и качеств.
Решая задачу разработки автоматической системы наведения зенитного орудия, Норберт Винер разрабатывает модель управления на основе нового прочтения понятий о «прямой» и «обратной» связи, а в конце 40-х обобщает свои представления в программе создания новой дисциплины – кибернетики.
В этот же период получает второе дыхание так называемый «системный подход» как междисциплинарный язык описания сложных технических и органических систем.
Умберто Матурана и Франциско Варела в своей книге «Древо познания» (1987) для описания этих систем употребили не очень понятный на русском языке термин «ауто-поэзиса»38.
38. Франциско В., Матурана У. «Древо познания. Биологические корни человеческого понимания». М., 2019.
Подобные системы, по мнению этих авторов, стремятся сохранять свою динамическую организацию и «самовоспроизводить» совокупность внутренних отношений между своими элементами.
На рубеже XXI века возрос интерес к феноменам рефлексии, самоорганизации и самоуправления органических систем, которые и должны стать предметом следующего «витка» нормативного описания и операционализации.
На передний рубеж выдвигаются задачи создания умных машин нового поколения — машинизации и автоматизации рефлексии как особого типа «обратных связей».